NEW TYPES OF SOFT SETS:
HyperSoft Set,
IndetermSoft Set, IndetermHyperSoft Set, SuperHyperSoft Set, TreeSoft Set
(An Improved Version)
The Soft Set was introduced by Molodtsov [1] in 1999.
Further on, four new types of Soft Sets, such as: the HyperSoft Set (2018), IndetermSoft Set (2022), IndetermHyperSoft Set (2022), and TreeSoft Set (2022), were introduced by Smarandache [2-7].
Let's recall their definitions together with real examples.
Definition of Soft Set
Let U be a universe of discourse, P(U) the power set of U, and A a set of attributes. Then, the pair (F, U), where F: A → P(U) is called a Soft Set over U.
Real Example of Soft Set
Let U = {Helen, George, Mary, Richard} and a set M = {Helen, Mary, Richard} included in U.
Let the attribute be: a = size, and its attribute’ values respectively:
Size = A1 = {small, medium, tall},
Let the function be: F: A1 → P(U).
Then, for example:
F(tall) = {Helen, Mary}, which means that both, Helen and Mary, are tall.
1. Definition of IndetermSoft Set
Let U be a universe of discourse, H a non-empty subset of U, and P(H) be the powerset of H. Let a be an attribute, and A be a set of this attribute-values. Then F: A → P(H) is called an IndetermSoft Set if at least one of the bellow occurs:
i) the set A has some indeterminacy;
ii) at least one of the sets H or P(H) has some indeterminacy;
iii) the function F has some indeterminacy, i.e. there exist at least one relationship F(a) = M, such that at least one of a or M has some indeterminacy (not unique, unclear, incomplete, unknown, etc.).
IndetermSoft Set, as extension of the classical (determinate) Soft Set, deals with indeterminate data, because there are sources unable to provide exact or complete information on the sets A, H, or P(H), nor on the function F. We did not add any indeterminacy, we found the indeterminacy in our real world. Because many sources give approximate/uncertain/incomplete/conflicting information, not exact information as in the Soft Set, as such we still need to deal with such situations.
Herein, ‘Indeterm’ stands for ‘Indeterminate’ (uncertain, conflicting, incomplete, not unique outcome, unknown).
Similarly, distinctions between determinate and indeterminate operators are taken into consideration. Afterwards, an IndetermSoft Algebra is built, using a determinate soft operator (joinAND), and three indeterminate soft operators (disjoinOR, exclussiveOR, NOT), whose properties are further on studied.
Smarandache has generalized the Soft Set to the HyperSoft set by transforming the function F into a multi-attribute function, and then he introduce the hybrids of Crisp, Fuzzy, Intuitionistic Fuzzy, Neutrosophic, other fuzzy extensions, and Plithogenic HyperSoft Set.
The classical Soft Set is based on a determinate function (whose values are certain, and unique), but in our world there are many sources that, because of lack of information or ignorance, provide indeterminate (uncertain, and not unique – but hesitant or alternative) information. They can be modeled by operators having some degree of indeterminacy due to the imprecision of our world.
Real Example of IndetermSoft Set
Assume a town has many houses.
1) Indeterminacy with respect to the set A of attributes.
You ask the source:
- What are all colors of the houses?
The source: I know for sure that there are houses of colors red, yellow, and blue, but I do not know if there are houses of other colors (?)
2) Indeterminacy with respect to the set H of houses.
You ask the source:
- How many houses are in the town?
The source:
- I never counted them, but I estimate their number to be between 100-120 houses.
3) Indeterminacy with respect to the function.
3a) You ask a source:
- What houses have the red color in the town?
The source:
- I am not sure, I think the houses h1 or h2.
Therefore, F(red) = h1 or h2 (indeterminate / uncertain answer).
3b) You ask again:
- But, what houses are yellow?
The source: - I do not know, the only thing I know is that the house h5 is not yellow because I have visited it.
Therefore, F(yellow) = not h5 (again indeterminate / uncertain answer).
3c) Another question you ask:
- Then what houses are blue?
The source:
- For sure, either h8 or h9.
Therefore, F(blue) = either h8 or h9 (again indeterminate / uncertain answer).
This is the IndetermSoft Set.
2. Definition of HyperSoft Set
The soft set was extended to the hypersoft set by transforming the function F into a multi-attribute function. Afterwards, the hybrids of HyperSoft Set with the Crisp, Fuzzy, Intuitionistic Fuzzy, Neutrosophic, other fuzzy extensions, and Plithogenic Set were introduced.
Let U be a universe of discourse, P(U) the power set of U. Let a1 , a2 , … , an, for n ≥ 1, be n distinct attributes, whose corresponding attribute values are respectively the sets A1 , A2 , … , An, with Ai ∩ Aj = Φ, for i ≠ j, and i,j in {1, 2, … , n}. Then the pair (F, A1 × A2 × … × An ), where F: A1 × A2 × … × An → P(U), is called a HyperSoft Set over U.
Real Example of HyperSoft Set
Let U = {Helen, George, Mary, Richard} and a set M = {Helen, Mary, Richard} included in U.
Let the attributes be: a1 = size, a2 = color, a3 = gender, a4 = nationality, and their attributes’ values respectively:
Size = A1 = {small, medium, tall},
Color = A2 = {white, yellow, red, black},
Gender = A3 = {male, female},
Nationality = A4 = {American, French, Spanish, Italian, Chinese}.
Let the function be: F: A1 × A2 × A3 × A4 → P(U).
Then, for example:
F({tall, white, female, Italian}) = {Helen, Mary}, which means that both, Helen and Mary, are tall and white and female and Italian.
Notice that this is an extension of the previous Real Example of Soft Set.
3. Definition of IndetermHyperSoft Set
Let U be a universe of discourse, H a non-empty subset of U, and P(H) the powerset of H. Let a1 , a2 , … , an, for n ≥ 1, be n distinct attributes, whose corresponding attribute-values are respectively the sets A1 , A2 , … , An, with Ai ∩ Aj = Φ for i ≠ j, and i, j in {1, 2, … , n}. Then the pair (F, A1 × A2 × … × An ), where F: A1 × A2 × … × An → P(H), is called an IndetermHyperSoft Set over U if at least one of the bellow occurs:
i) at least one of the sets A1 , A2 , … , An has some indeterminacy;
ii) at least one of the sets H or P(H) has some indeterminacy;
iii) the function F has some indeterminacy, i.e. there exist at least a relationship F(e1, e2, …, en) = M such that at least one of e1, a2, …, en, or M is indeterminate (unclear, uncertain, conflicting, or not unique, unknown, etc.).
Similarly, IndetermHyperSoft Set is an extension of the HyperSoft Set, when there is indeterminate data, or indeterminate function, or indeterminate sets.
Real Example of IndetermHyperSoft Set
Assume a town has many houses.
1) Indeterminacy with respect to the product set A1 × A2 × … × An of attributes.
You ask the source:
- What are all colors and sizes of the houses?
The source: I know for sure that there are houses of colors of red, yellow, and blue, but I do not know if there are houses of other colors (?) About the size, I saw many houses that are small, but I do not remember to have seeing big houses.
2) Indeterminacy with respect to the set H of houses.
You ask the source:
- How many houses are in the town?
The source:
- I never counted them, but I estimate their number to be between 100-120 houses.
3) Indeterminacy with respect to the function.
3a) You ask a source:
- What houses are of red color and big size in the town?
The source:
- I am not sure, I think the houses h1 or h2.
Therefore, F(red, big) = h1 or h2 (indeterminate / uncertain answer).
3b) You ask again:
- But, what houses are yellow and small?
The source:
- I do not know, the only thing I know is that the house h5 is neither yellow nor small because I have visited it.
Therefore, F(yellow, small) = not h5 (again indeterminate / uncertain answer).
3c) Another question you ask:
- Then what houses are blue and big?
The source:
- For sure, either h8 or h9.
Therefore, F(blue, big) = either h8 or h9 (again indeterminate / uncertain answer).
This is the IndetermHyperSoft Set.
4. Definition of SuperHyperSoft Set
The SuperHyperSoft Set is an extension of the HyperSoft Set.
As for the SuperHyperAlgebra, SuperHyperGraph, SuperHyperTopology and in general for SuperHyperStructure and Neutrosophic SuperHyperStructure (that includes indeterminacy) in any field of knowledge, “Super” stands for working on the powersets (instead of sets) of the attribute value sets.
Let U be a universe of discourse, P(U) the power set of U. Let a1 , a2 , … , an, for n ≥ 1, be n distinct attributes, whose corresponding attribute values are respectively the sets A1 , A2 , … , An, with Ai ∩ Aj = Φ, for i ≠ j, and i,j in {1, 2, … , n}. Let P(A1) , P(A2) , … , P(An) be the powersets of of the sets A1 , A2 , … , An respectively.
Then the pair ( F, P(A1) × P(A2) × … × P(An) ), where F: P(A1) × P(A2) × … × P(An) → P(U), where × means Cartesian product, is called a SuperHyperSoft Set over U.
Real Example of SuperHyperSoft Set
If we define the function: F: P(A1) × P(A2) × P(A3) × P(A4) → P(U), we get a SuperHyperSoft Set.
Let’s assume, from the previous example, that:
F({medium,tall},{white, red, black},{female},{American, Italian}) = {x1 , x2} , which means that:
F( {medium or tall} and {white or red or black} and {female} and {American or Italian} ) = {x1 , x2}.
Therefore, the SuperHyperSoft Set offers a larger variety of selections, so x1 and x1 may be:
either medium, or tall (but not small),
either white, or red, or black (but not yellow),
mandatory female (not male),
and either American, or Italian (but not French, Spanish, Chinese).
5. Definition of TreeSoft Set
Let U be a universe of discourse, and H a non-empty subset of U, with P(H) the powerset of H.
Let A be a set of attributes (parameters, factors, etc.),
A= {A1 , A2 , … , An}, for integer n ≥ 1, where A1 , A2 , … , An are considered attributes of first level (since they have one-digit indexes).
Each attribute Ai, 1 ≤ i ≤ n, is formed by sub-attributes:
A1= {A1,1 , A1,2 , … }
A2= {A2,1 , A2,2 , … }
.........................
An= {An,1 , An,2 , … }
where the above Ai,j are sub-attributes (or attributes of second level) (since they have two-digit indexes).
Again, each sub-attribute Ai,j is formed by sub-sub-attributes (or attributes of third level):
Ai,j,k
And so on, as much refinement as needed into each application, up to sub-sub-…-sub-attributes (or attributes of m-level (or having m digits into the indexes):
Ai1,i2,...,im
Therefore, a graph-tree is formed, that we denote as Tree(A), whose root is A (considered of level zero), then nodes of level 1, level 2, up to level m.
We call leaves of the graph-tree, all terminal nodes (nodes that have no descendants).
Then the TreeSoft Set is:
F: P(Tree(A)) → P(H)
Tree(A) is the set of all nodes and leaves (from level 1 to level m) of the graph-tree, and P(Tree(A)) is the powerset of the Tree(A).
All node sets of the TreeSoft Set of level m are:
Tree(A) = {Ai1| i1= 1, 2, ... }
The first set is formed by the nodes of level 1, second set by the nodes of level 2, third set by the nodes of level 3, and so on, the last set is formed by the nodes of level m. If the graph-tree has only two levels (m = 2), then the TreeSoft Set is reduced to a MultiSoft Set [8].
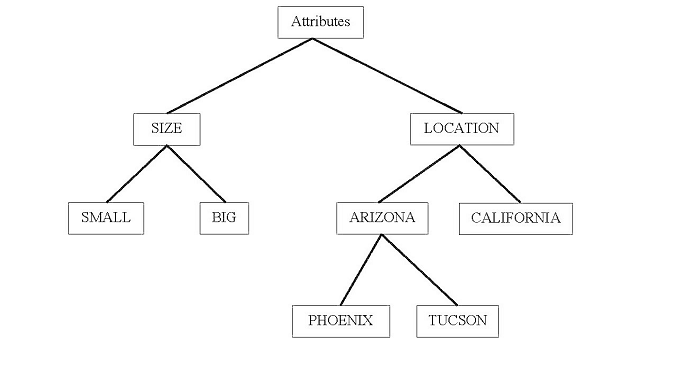
Practical Example of TreeSoft Set of Level 3
This is a classical tree, whose:
Level 0 (the root) is the node Attributes;
Level 1 is formed by the nodes: Size, Location;
Level 2 is formed by the nodes Small, Big, Arizona, California;
Level 3 is formed by the nodes Phoenix, Tucson.
Let’s consider H = {h1, h2, ..., h10} be a set of houses, and P(H) the powerset of H.
And the set of Attributes: A = {A1, A2}, where A1 = Size, A2 = Location.
Then A1 = {A11, A12} = {Small, Big}, A2 = {A21, A22} = {Arizona, California} as American states.
Further on, A22 = {A211, A212} = {Phoenix, Tucson} as Arizonian cities
Let’s assume that the function F gets the following values:
F(Big, Arizona, Phoenix} = { h9, h10 }
F(Big, Arizona, Tucson) = { h1, h2, h3, h4 }
F(Big, Arizona) = all big houses from both cities, Phoenix and Tucson
= F(Big, Arizona, Phoenix) ∪ F(Big, Arizona, Tucson) = { h1, h2, h3, h4, h9, h10 }.
Conclusion
The HyperSoft Set (2018) is a generalization of Soft Set (1999), from a uni-variate function to a multi-variate function F;
IndetermSoft Set (2022) is an extension of the Soft Set, from the determinate data to indeterminate data;
IndetermHyperSoft Set (2022) is an extension of the HyperSoft Set, from the determinate data to indeterminate data;
SuperHyperSoft Set (2023) is a generalization of the HyperSoft Set, where one considers the powersets of the attribute value sets;
and TreeSoft Set (2022) is a generalization of the MultiSoft Set that is a subclass of the HyperSoft Set.
References
1. Molodtsov, D. (1999) Soft Set Theory First Results. Computer Math. Applic. 37, 19-31
2. F. Smarandache, Extension of Soft Set to Hypersoft Set, and then to Plithogenic Hypersoft Set, Neutrosophic Sets and Systems, vol. 22, 2018, pp. 168-170 DOI: 10.5281/zenodo.2159754; http://fs.unm.edu/NSS/ExtensionOfSoftSetToHypersoftSet.pdf
3. Florentin Smarandache, Extension of Soft Set to Hypersoft Set, and then to Plithogenic Hypersoft Set (revisited), Octogon Mathematical Magazine, vol. 27, no. 1, April 2019, pp. 413-418
4. Florentin Smarandache, Introduction to the IndetermSoft Set and IndetermHyperSoft Set, Neutrosophic Sets and Systems, Vol. 50, pp. 629-650, 2022 DOI: 10.5281/zenodo.6774960; http://fs.unm.edu/NSS/IndetermSoftIndetermHyperSoft38.pdf
5. F. Smarandache, (2015). Neutrosophic Function, in Neutrosophic Precalculus and Neutrosophic Calculus, EuropaNova, Brussels, 14-15, 2015; http://fs.unm.edu/NeutrosophicPrecalculusCalculus.pdf
6. F. Smarandache, Neutrosophic Function, in Introduction to Neutrosophic Statistics, Sitech & Education Publishing, 74-75, 2014; http://fs.unm.edu/NeutrosophicStatistics.pdf
7. F. Smarandache, Soft Set Product extended to HyperSoft Set and IndetermSoft Set Product extended to IndetermHyperSoft Set, Journal of Fuzzy Extension and Applications, 2022, DOI: 10.22105/jfea.2022.363269.1232, http://fs.unm.edu/TSS/SoftSetProduct.pdf
8. Shawkat Alkhazaleh, Abdul Razak Salleh, Nasruddin Hassan, Abd Ghafur Ahmad, Multisoft Sets, Proc. 2nd International Conference on Mathematical Sciences, pp. 910-917, Kuala Lumpur, Malaysia, 2010.
9. F. Smarandache, New Types of Soft Sets: HyperSoft Set, IndetermSoft Set, IndetermHyperSoft Set, and TreeSoft Set, International Journal of Neutrosophic Science, Vol. 20 , No. 4, (2023) : 58-64, http://fs.unm.edu/TSS/NewTypesSoftSets-IJNS.pdf
10. Florentin Smarandache, New Types of Soft Sets ”HyperSoft Set, IndetermSoft Set, IndetermHyperSoft Set, and TreeSoft Set”: An Improved Version, Neutrosophic Systems with Applications, 35-41, Vol. 8, 2023, http://fs.unm.edu/TSS/NewTypesSoftSets-Improved.pdf.
11. Florentin Smarandache, Foundation of the SuperHyperSoft Set and the Fuzzy Extension SuperHyperSoft Set: A New Vision, Neutrosophic Systems with Applications, Vol. 11, 48-51, 2023, Neutrosophic Systems with Applications, Vol. 11, 48-51, 2023, http://fs.unm.edu/TSS/SuperHyperSoftSet.pdf.
12. Ali Alqazzaz and Karam M. Sallam, A TreeSoft Set with Interval Valued Neutrosophic Set in the era of
Industry 4.0, Neutrosophic Sets and Systems, Vol. 64, 2024, pp. 170-184. DOI: 10.5281/zenodo.10729973
13. F.Smarandache, Practical Applications of IndetermSoft Set and IndetermHyperSoft Set and Introduction to
TreeSoft Set as an extension of the MultiSoft Set, Neutrosophic Sets and Systems, Vol. 51, 2022, pp. 939-
947. DOI : 10.5281/zenodo.7154238
14. Florentin Smarandache, Mona Mohamed, and Michael Voskoglou, Evaluating Blocking Blockchain Based on Tree Soft
and Opinion Weight Criteria Method under Uncertainty Climate, HyperSoft Set Meth. Eng. Vol. 1 (2024) 1–10.
15. G. Dhanalakshmi, S. Sandhiya, F. Smarandache, Selection of the best process for desalination under a TreeSoft
Setenvironment using the multi-criteria decision-making method, International Journal of Neutrosophic Science (IJNS),
Vol. 23, No. 03, PP. 140-147, 2024.