On the Pseudo-Smarandache Function

By

J. Sándor

Babes-Bolyai Univ., 3400 Cluj, Romania

Kashihara[2] defined the "Pseudo-Smarandache" function Z by

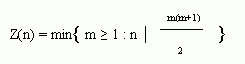
Properties of this function have been studied in [1], [2] etc.

1. By answering a question by C. Ashbacher, Maohua Le proved that S(Z(n)) - Z(S(n)) changes signs infinitely often. Put

We will prove first that

and

implying (1) . We note that if the equation S(Z(n)) = Z(S(n)) has infinitely many solutions, then clearly the lim inf in (1) is 0, otherwise is 1, since

| S(Z(n)) - Z(S(n)) | >= 1, S(Z(n)) - Z(S(n)) being an integer.

This inequality is best possible for even n, since Z(2^k) = 2^k+1 - 1. We note that for odd n, we have Z(n) <= n - 1, and this is best possible for odd n, since Z(p) = p-1 for prime p.

By

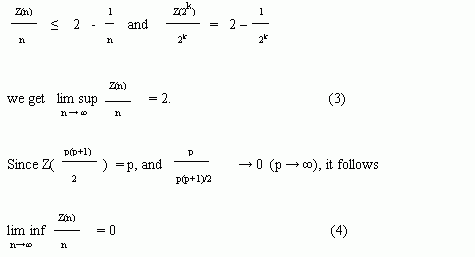
On the other hand, by Z(Z(n)) <= 2Z(n) - 1 and (3), we have

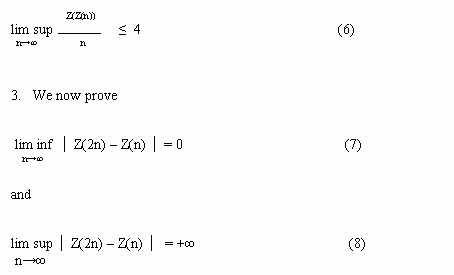
Indeed, in [1] it was proved that Z(2p) = p-1 for a prime p congruent to 1 modulo 4. Since Z(p) = p-1, this proves relation (7).

On the other hand, let n = 2^k. Since Z(2^k) = 2^k+1 - 1 and Z(2^k+1) = 2^k+2 - 1, clearly Z(2^k+1) - Z(2^k) = 2^k+1 -> infinity as k -> infinity.

References

1. C. Ashbacher, The Pseudo-Smarandache Function and the Classical Functions of Number Theory, Smarandache Notions J., 9(1998), No. 1-2, 78-81.
2. K. Kashihara, Comments and Topics on Smarandache Notions and Problems, Erhus Univ. Press, AZ., 1996.
3. M. Bencze, OQ. 351, Octogon M.M. 8(2000), No. 1, p. 275.
4. J. Sándor, On Certain New Inequalities and Limits for the Smarandache Function, Smarandache Notions J., 9(1998), No. 1-2, 63-69.
5. J. Sándor, On the Difference of Alternate Compositions of Arithmetical Functions, to appear.