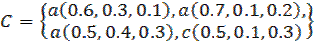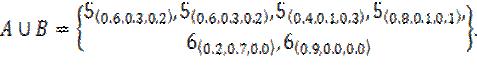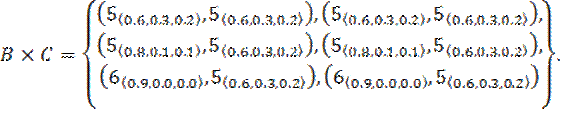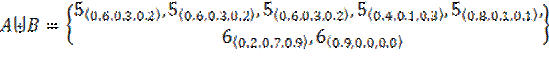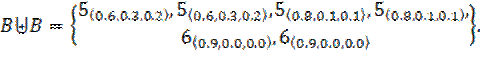NEUTROSOPHIC MULTISET STRUCTURES
![]()
The Neutrosophic Multisets and the Neutrosophic Multiset Algebraic Structures were introduced
by Florentin Smarandache [2, 3, 4] in 2016.
1. Definition of Neutrosophic Multiset
Let
be a universe of discourse, and
.
A Neutrosophic Multiset is a neutrosophic set where one or more elements are repeated
with the same neutrosophic components, or with different neutrosophic components.
2. Examples
is a neutrosophic set (not a neutrosophic multiset).
But
is a neutrosophic multiset, since the element a is repeated; we say that the element a has
neutrosophic multiplicity 2 with the same neutrosophic components.
While
is also a neutrosophic multiset, since the element a is repeated (it has neutrosophic
multiplicity 3), but with different neutrosophic components, since, for example, during
the time, the neutrosophic membership of an element may change.
If the element is repeated times keeping the same neutrosophic components
,
we say that a has multiplicity .
But if there is some change in the neutrosophic components of a, we say that a has the
neutrosophic multiplicity .
Therefore, we define in general the Neutrosophic Multiplicity Function:
where
,
and for any
one has
which means that a is repeated
times with the neutrosophic components
;
a is repeated
times with the neutrosophic components
, ..., a is repeated

times with the neutrosophic components
, ..., and so on.
Of course, all
, and
, for
, with
.
Also, all neutrosophic components are with respect to the set . Then, a neutrosophic
multiset A can be written as:
or
.
3. Examples of operations with neutrosophic multisets.
Let's have:
Then:
1.3.1. Intersection of Neutrosophic Multisets.
1.3.2. Union of Neutrosophic Multisets.
1.3.3. Inclusion of Neutrosophic Multisets.
, but
4. Cardinality of Neutrosophic Multisets.
, and
3, where
means cardinal.
5. Cartesian Product of Neutrosophic Multisets.
6. Difference of Neutrosophic Multisets.
7. Sum of Neutrosophic Multisets.
Let's compute the neutrosophic multiplicity function, with respect to several of the
previous neutrosophic multisets.
.
References
[1] Eric W. Weisstein, Multiset, MathWorld, CRC Encyclopedia of Mathematics,
Boca Raton, FL, USA.
[2] F. Smarandache, Neutrosophic Theory and Applications, Le Quy
Don Technical University, Faculty of Information technology,
Hanoi, Vietnam, 17th May 2016.
[3] F. Smarandache, Neutrosphic Multiset Applied in Physical Processes,
Actualization of the Internet of Things, a FIAP Industrial Physics Conference,
Monterey, California, Jan. 2017.
[4] F. Smarandache, Neutrosophic Perspectives: Triplets, Duplets, Multisets,
Hybrid Operators, Modal Logic, Hedge Algebras. And Applications. Pons
Editions, Bruxelles, 323 p., 2017;
120-121 Neutrosophic Complex Multiset: 122-123.Neutrosophic Multiset: 115-119
Neutrosophic Multiset Applied in Physical Processes:
![]()