Resolucion de sistemas de ecuaciones

Resolucion de sistemas de ecuaciones lineales neutrosóficas mediante computación simbólica.
Solving neutrosophic linear equations systems using symbolic computation.
Maikel Leyva-Vázquez1 , Florentin Smarandache2
1 Universidad Politecnica Salesiana, Guayaquil Ecuador. Email: mleyvaz@gmail.com
2 Mathematics & Science Department, University of New Mexico. 705 Gurley Ave., Gallup, NM 87301, USA. e-mail: fsmarandache@gmail.com
Resumen. En este trabajo, aplicamos el concepto de números neutrosóficos para resolver un sistema de ecuaciones lineales neutroficas que utilizan la computación simbólica. Además, utilizamos Jupyter, que es apoyado en el Colaborador de Google para realizar el cómputo simbólico. La biblioteca simbólica de Python se utiliza para realizar el proceso de computación neutrosófica. Los sistemas de ecuaciones lineales neutrosóficas se resuelven a través de la computación simbólica en Python. Se ha desarrollado un estudio de caso para la determinación del tráfico vehicular con indeterminación. Este rey de la computación abre nuevas formas de tratar la indeterminación en problemas del mundo real.
Palabras claves: Computación neutrosófica, sympy, google colaborativo, número neutrosófico, ecuaciones lineales Neutrosóficas.
Abstract. In this paper, we apply the concept of neutrosophic numbers to solve a systems of neutrophic linear equations using symbolic computation. Also, we utilize Jupyter, which is supported in Google Colaboratory for performing symbolic computation. The sympy library of Python is used to perform the process of neutrosophic computation. Systems of neutrosophic linear equations are solved through symbolic computation in Python. A case study was developed for the determination of vehicular traffic with indeterminacy. This king of computation opens new ways to deal with indeterminacy in real-world problems.
Keywords: neutrosophic computing, sympy, google colaboratory, neutrosophic number, neutrosophic linear equations
INTRODUCCIÓN
The word Neutrosophy means knowledge of neutral thought, and this third / neutral represents the main distinction, i.e., the neutral/indeterminate / unknown part (in addition to "truth" / "belonging" and "falsehood" Components of "non-belonging" that appear in the fuzzy logic / set). Neutrosophic logic (NL) is a generalization of Zadeh's fuzzy logic (FL), and especially of Atanassov's intuitionistic fuzzy logic (IFL), and other multi-valued logics, see Figure 1 and [1].
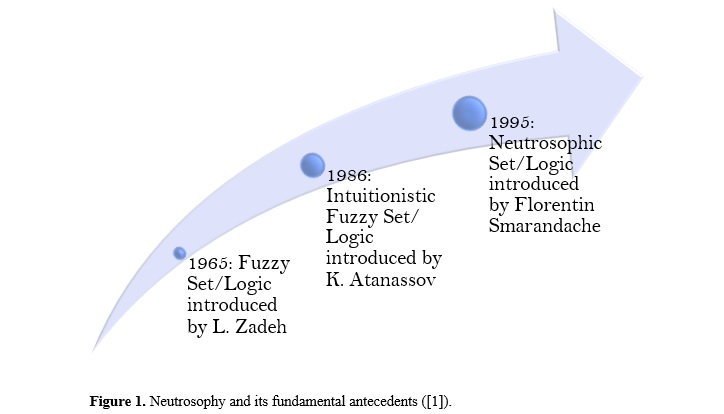
Let U be a universe of discourse, and M a set included in U. An element x of U which is denoted with respect to M as x (T, I, F) and belongs to M according to the Neutrosophic Set as follows: it is t % true in the set, i% indeterminate (unknowns) in the set, and f% false, where t varies in T, i varies in I and f varies in F. Statically T, I, F are subsets, but dynamically T, I, F are functions/operators that depend on many known or unknown parameters [2, 3].
Neutrosophic sets generalize the fuzzy sets (especially the fuzzy and fuzzy intuitionist sets), the paraconsistent sets. It allows dealing with a more significant number of situations that occur in real-life [4].
- PRELIMINARY
A statistical neutrosophic number is a number given in the following form ([5]):
N=d+i (1)
Where d is the determined part and i is the indeterminate part, see [6]. For example: a=8.6+i if iÎ[3, 3.4] the number is equivalent to aÎ [11.6, 12].
Additionally, a neutrosophic matrix is a matrix such that the elements a = (aij) have been replaced by elements in <RÈI>, where <RÈI> is a neutrosophic ring, see [7].
A neutrosophic graph is a kind of graph in which at least one arc is a neutrosophic arc, see [8]. The weights associated with the arcs have the following meanings: 0 = “no connection between nodes”, 1 = “connection between nodes”, I = “indeterminate connection (unknown if it is or not)”. The neutrosophic adjacency matrix is an adjacency matrix with at least one neutrosophic arc. Such notions are not used in fuzzy theory, an example of which is shown below:
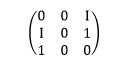
Further, we shall describe practical implementations of this approach. Google Colaboratory is a web application that allows us to create and share documents containing source codes, equations, visualizations, and illustrative texts, as shown in Figure 2.
Figure 2. Google Colaboratory
Jupyter allows us to interact with several programming languages; in this case, Python is used. Python is a simple and powerful programming language with access to a great variety of useful libraries.
- NEUTROSOPHIC COMPUTING AND SYMPY
SymPy can be used for computational works with neutrosophic numbers in Python language. It is a library written in Python language with the purpose of bringing together all the features of a computer algebra system, which is easily extensible and maintains the code as simple as possible ([9]).
Here we propose a calculus that is based on interval-valued arithmetic and accordingly, a de-neutrosification process is required [10] to obtain a representative numeric value. Thus, I Î[0,1] is replaced by its maximum and minimum values.
In this case we employ the mpmath library and the mpi type [11]. The mpi type deals with intervals of a pair of mpf values. Interval arithmetic uses conservative rounding, so that, if an interval is interpreted as the numerical uncertainty with respect to a single-valued number, any sequence of interval operations will produce intervals that contain the result of applying the same sequence of operations to a precise number, see Figure 3.
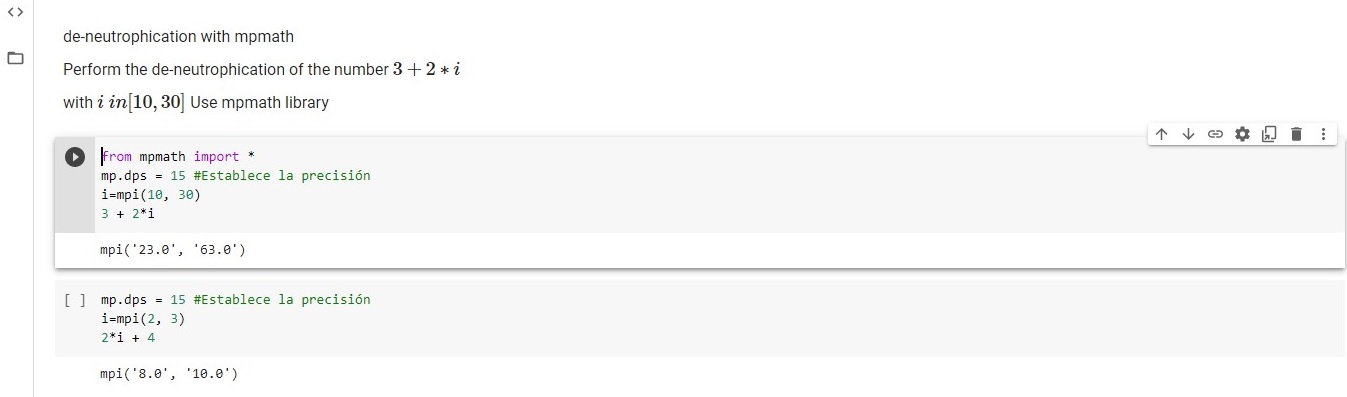
Figure 3. Working with Neutrosophic Numbers
In this case systems of neutrosophic linear equations can be solved, see [12]. For example, given the following system of equations:
3x+8y = 1+i (2)
4x + 7y = 8+i (3)
It is solved as follows, see Figure 4:
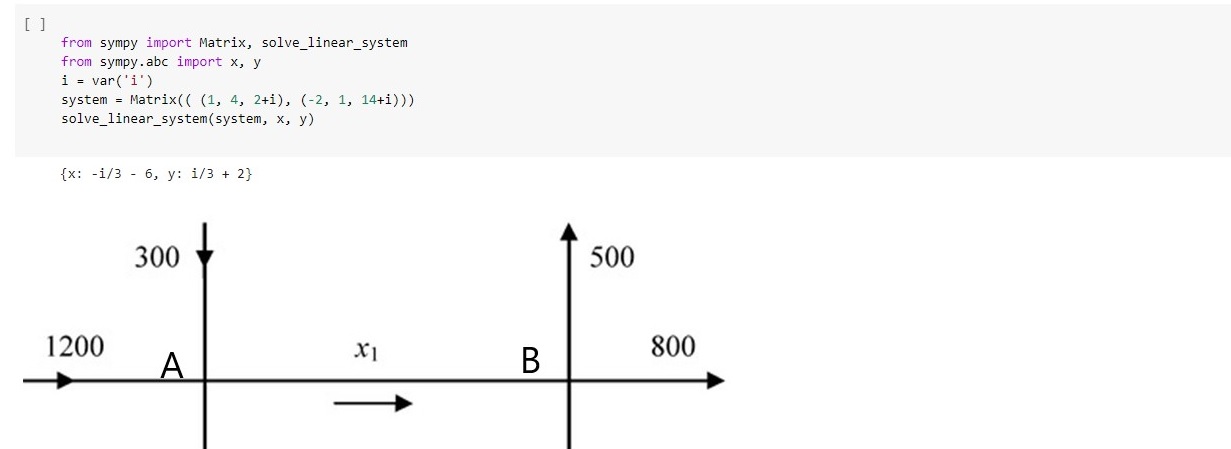
Figure 4. Solution to a system of linear equations with Neutrosophic Numbers, by using Colaboratory.
An example of application in a real-life problem is a system of linear equations that determines the flow of traffic at different intercepts, see Figure 5
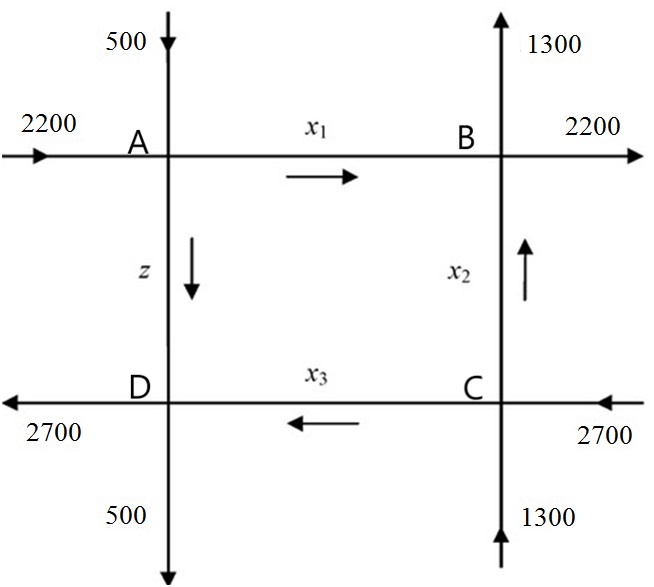
Figure 5. Schematic representation of the Vehicle Flow ([12]).
At each intercept, the outflow must be equal to the inflow.
Intercept A: 2700=x1+z
Intercept B: 3500=x1+x2
Intercept C: 4000=x2+x3
Interception D: 3200=x3+z
If z=500.
Then the system of equations is as follows:
x1=2200
x1+x2=3500
x2+2x3=6700
The solution for this system is the following:
x1=2200
x2=1300
x3=2700

Figure 6. A solution of the vehicular flow with indetermination.
In the case of z =500+i.
Then the system of equations is:
x1=2200-i
x1+x2=3500
x1+2x3=6700-i
The solution for this system is:
x1=2200-i
x2=1300+i
x3=2250
This kind of computation allows opening new ways to compute using indeterminacy in different real-world problems [13-19].
CONCLUSIONES
In this paper, the concept of neutrosophic numbers was used to solve linear equations. The tool Jupyter supported by Google Colaboratory is utilized. The Sympy library is applied to perform the neutrosophic computation process. Neutrosophic linear equation systems are solved by symbolic python computation. A case study is developed for the determination of vehicular traffic with indetermination.
Future works include the development of new applications in different areas of engineering and science like neutrosophic statistics and multicriteria. Other areas of future work include the development of new tools for neutrosophic computing.
REFERENCIAS
M. Leyva-Vázquez and F. Smarandache. “Artificial Intelligence: Challenges, Perspectives and the Role of Neutrosophy” (Master Conference): Contemporary Dilemmas: Education, Politics and Values, vol. 6, no. Special, pp. 1-15, 2018.
M. Leyva-Vázquez et. al. Métodos multicriterios para determinar de la efectividad de la gestión pública y el análisis de la transparencia. Pons Publishing House, 2018.
R. Escobar. et al. “Facebook as a Tool to Promote Socialization in Traditional Artificial Intelligence Courses. Calculation of engagement using neutrosophic triangular neutrosophic numbers neutrosophic” Computing and Machine Learning, vol. 2, pp. 9-21, 2018.
N. Batista and J. Estupiñán. Gestión Empresarial y Posmodernidad. Infinite Study, 2018.
F. Smarandache. Introduction to neutrosophic statistics. Infinite Study, 2014.
N. Batista et al. “Validation of the pedagogical strategy for the formation of the competence entrepreneurship in high education through the use of neutrosophic logic and Iadov technique”, Neutrosophic Sets and Syst, vol. 23, pp. 45-52, 2018.
W.V. Kandasamy, and F. Smarandache. Fuzzy Neutrosophic Models for Social Scientists. Education Publisher Inc., 2013.
W.V. Kandasamy, and F. Smarandache, Fuzzy cognitive maps and neutrosophic cognitive maps. American Research Press, 2003.
A. Meurer et al. “SymPy: symbolic computing in Python” Peer J Computer Science, vol. 3, pp.e103, 2017. Available at: https://doi.org/10.7717/peerj-cs.103.
J. L. Salmeron and F. Smarandache. “Redesigning Decision Matrix Method with an indeterminacy-based inference process”. J. Appl. Math. Stat, vol. 13, no. M08, pp. 4-11, 2008.
F. Johansson.(2013, December) mpmath: a Python library for arbitrary-precision floating-point arithmetic (version 0.18), December, 2013 [Online] Official Wiki Page available at: http://code. google. com/p/mpmath.
J. Ye, “Neutrosophic Linear Equations and Application in Traffic Flow Problems” Algorithms, vol. 10, no. 4, pp. 133, 2017.
Gómez, G.Á., J.V. Moya, J.E. Ricardo, and C.B.V. Sanchez, Evaluating Strategies of Continuing Education for Academics Supported in the Pedagogical Model and Based on Plithogenic Sets. Neutrosophic Sets and Systems, 2020. 37(1): p. 3.
Ricardo, J.E., N.B. Hernández, R.J.T. Vargas, A.V.T. Suntaxi, and F.N.O. Castro, La perspectiva ambiental en el desarrollo local. Dilemas contemporáneos: Educación, Política y Valores, 2017.
Smarandache, F., M.A. Quiroz-Martínez, J.E. Ricardo, N.B. Hernández, and M.Y.L. Vázquez, Application of neutrosophic offsets for digital image processing. 2020: Infinite Study.
Smarandache, F., J.E. Ricardo, E.G. Caballero, M. Yelandi, L. Vázquez, and N.B. Hernández, Delphi method for evaluating scientific research proposals in a neutrosophic environment. Neutrosophic Sets and Systems, 2020: p. 204.
Leyva-Vázquez, M. and F. Smarandache, Computación neutrosófica mediante Sympy Neutrosophic Computing with Sympy. Neutrosophic Computing and Machine Learning: p. 16.
BATISTA HERNÁNDEZ, N. and J. ESTUPIÑÁN RICARDO, Gestion empresarial y posmodernidad: Infinite Study. 2018, Pons Publishing House, Bruxelles.
Estupiñán Ricardo, J., Á.B. Martínez Vásquez, R.A. Acosta Herrera, A.E. Villacrés Álvarez, J.I. Escobar Jara, and N. Batista Hernández, Sistema de Gestión de la Educación Superior en Ecuador. Impacto en el Proceso de Aprendizaje. Dilemas Contemporáneos: Educación, Política y Valores, 2018.
Fecha de Recepción: 25 de Noviembre De 2020 Fecha de Aceptación: 24 de Diciembre 2020



















