Optimizing Network Structures Through Neutrosophic Graph Product Operations and its  Coloring: A Comprehensive Approach for Enhanced Connectivity and Robustness

A. Meenakshi; S. Dhanushiya

Authors

A. Meenakshi Department of Mathematics, Vel Tech Rangarajan Dr. Sagunthala R&D Institute of Science and Technology; Chennai-600 062, India
S. Dhanushiya Department of Mathematics, Vel Tech Rangarajan Dr. Sagunthala R&D Institute of Science and Technology; Chennai-600 062, India

Keywords:

Neutrosophic graph, vertex order coloring, co-normal, tensor, residue

Abstract

Optimal network analysis requires advanced techniques to handle the inherent complexity and
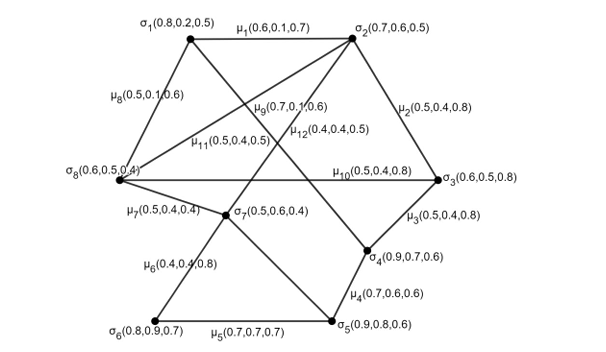
uncertainty of real-world systems. We have used vertex order coloring on neutrosophic graphs to
find the most effective approach to improve network reliability and performance. Neutrosophic
graphs( ) offer a comprehensive framework for modelling real-world networks with inherent
uncertainties by incorporating degrees of truth, falsity, and indeterminacy. In this paper, we have
investigated various graph product operations as a means of optimizing network structures. We
further investigated the applications of vertex order coloring to identify and
within various graph operations of . We examined several
strong vertices
products with the goal of
determining the most optimal network based on particular important metrics including the total
number of alpha-strong vertices, the weight of alpha-strong vertices, the chromatic number, and the
weight of the graph's minimum spanning tree. The objective of our research is to identify the best
solutions that strike a balance between robustness and association by rigorously studying and
comparing various product operations. Our research advances the subject of network theory and
provides useful information for a variety of applications, including social networks, transportation,
and telecommunications.