Solving Non-linear Neutrosophic Linear Programming Problems

Abstract

Non-linear neutrosophic numbers (NLNNs) are different kinds of neutrosophic numbers
with at least one non-linear membership function (either of truthiness, falsity or indeterminacy
part) of the information. Furthermore, a linear programming problem with non-linear
neutrosophic numbers as coefficients/parameters is a special type of programming problem known
as a non-linear linear programming problem (NLN-LPP). This paper elaborates on the concepts of
non-linear neutrosophic number (NLNN) sets, different forms of non-linear neutrosophic numbers
(NLNNs), 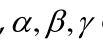cuts on non-linear neutrosophic numbers (NLNNs), possibility mean, possibility
standard deviation, and possibility variance of non-linear neutrosophic numbers (NLNNs). In this
paper, we also propose the solution technique for non-linear neutrosophic linear programming
problems (NLN-LPPs) in which all coefficients/parameters are non-linear neutrosophic numbers
(NLNNs). In this continuation, we suggest a new modified possibility score function for non-linear
NNs in terms of possibility means and possibility standard deviations of non-linear neutrosophic
numbers (NLNNs) for better use of all parts of information. This modified score function is used to
convert non-linear neutrosophic number (NLNN) coefficients/parameters of non-linear
neutrosophic linear programming problem (NLN-LPP) into equivalent crisp values. Thereafter, the
equivalent crisp problem is solved with the usual method to obtain the optimal solution of
non-linear neutrosophic linear programming problem (NLN-LPP). The proposed solution
algorithm is unique and new for solving non-linear neutrosophic linear programming problems. A
numerical example is solved with the proposed algorithm to legitimate the research output. A case
study is also discussed to show its applicability in solving real-life problems.