Decision Making By Neutrosophic Over Soft Topological Space

R.Narmada Devi; Yamini Parthiban

Authors

R.Narmada Devi Department of Mathematics, Vel Tech Rangarajan Dr.Sagunthala R&D Institute of Science and Technology, Avadi, Chennai, Tamil Nadu, India.;
Yamini Parthiban Department of Mathematics, Vel Tech Rangarajan Dr.Sagunthala R&D Institute of Science and Technology, Avadi, Chennai, Tamil Nadu, India.;

Keywords:

Neutrosophic Over Soft Set and Neutrosophic Over Soft Topological Space

Abstract

The empirical correlation system serves as a crucial tool for unveiling the linear interconnections
between two variables. Its significance lies in providing a prominent approach to depict a straightforward
relationship without explicitly indicating a causal link between the sets involved. In the current research,
an innovative concept of correlations is introduced specifically for Neutrosophic Over Soft Sets (No
s-sets).
This novel framework involves a meticulous examination of basic definitions and operations associated with
Neutrosophic Over Soft Sets. Furthermore, the study extends to the introduction of a groundbreaking concept:
a topological space integrated with Neutrosophic Over Soft Sets (No
s-sets). This addition aims to broaden
the scope of understanding and application in mathematical contexts.The research does not merely establish
theoretical foundations; it also explores various properties and theorems related to the introduced concepts. This
is complemented by a series of numerical examples designed to provide clarity and facilitate a comprehensive
grasp of the material. To demonstrate the practical application of these concepts, the research utilizes the
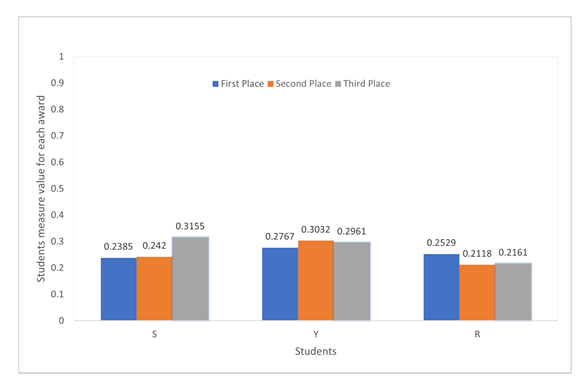
correlation framework to present a numerical illustration. Specifically, it is applied to determine the top
performing student at GFC School for the academic year 2022-2023, showcasing the real-world relevance and
applicability of the proposed methodologies