The Theoretical Framework on Approximation of Neutrosophic Numbers and Their Application

Augus Kurian; Sumathi I R; Omaima Al-Shanqiti

Authors

Augus Kurian Department of Mathematics, Amrita School of Physical Sciences, Coimbatore, Amrita Vishwa Vidyapeetham, India
Sumathi I R Department of Mathematics, Amrita School of Physical Sciences, Coimbatore, Amrita Vishwa Vidyapeetham, India
Omaima Al-Shanqiti Umm Al-Qura University, Department of Mathematics, Mekkah, Saudia Arabia;

Keywords:

Neutrosophic Number; Generalized Nonlinear Hexagonal Neutrosophic Number with asymmetry; Approximation; Expected Interval; Values; MCDM.

Abstract

Neutrosophic sets are effectual logic represented to understand ambiguous and inconsistent information. They are frequently used to explain many types of partial or incomplete information. Researchers
have given much attention to the decision-making theory and its associated methodologies based on uncertain
linguistic factors. This article emphasizes the novel neutrosophic number approximations to handle linguistic
variables and their application in multiple-attribute decision-making. Different approximation techniques are
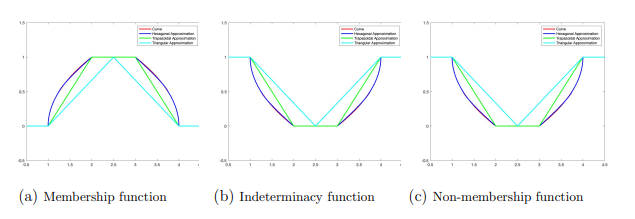
introduced in neutrosophic sets, but substantial data loss may occur. Hence, a hexagonal neutrosophic number
was proposed to deal with information loss during approximation. Also, the comparison study with existing
techniques is explored to show the effectiveness of the proposed approximation. The expected interval criterion
was retained although an approximation was made to give more desirable features. An MCDM (Multi-Criteria
Decision Making) problem is presented to demonstrate efficiency and simplicity with uncertain parameters.

DOI: 10.5281/zenodo.13955784