Neutrosophic Soft Sets in One And Two-Dimensions Using Iteration Method

M.N.Bharathi; G.Jayalalitha

Authors

M.N.Bharathi Research scholar Department of Mathematics Vels Institute of Science Technology and Advanced Studies;
G.Jayalalitha Professor Department of Mathematics Vels Institute of Science Technology and Advanced Studies;

Keywords:

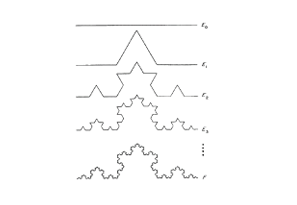
Fuzzy set, Neutrosophic soft set, Fractals, Von Koch curve, Sierpinski triangle.

Abstract

This paper introduces a different perspective of Neutrosophic Fractals and Neutrosophic Soft
Fractals, merging the principles of Neutrosophic Logic, Soft set theory, and Fractal Geometry to
address indeterminacy in complex, self-similar structures specifically the Von Koch curve and the
Sierpinski triangle. It sightsees the complex qualities of Neutrosophic soft sets by incorporating
attributes of falsification, indefiniteness, and truth into union and intersection operations. The
research elucidates the interplay between Neutrosophic Logic and fractal geometry, leading to
more precise modeling of complex systems. Proving theorems and providing examples examine
the intricate interactions between membership characteristics in these fractal structures,
demonstrating self-similarity. Fractal geometry is applied innovatively to improve the
representation of uncertainty, indeterminacy, and falsity in Neutrosophic Logic, enhancing
mathematical modeling techniques. Results show that the Sierpinski triangle provides a better
representation than the Koch curve.

DOI: 10.5281/zenodo.14538057