Neutrosophic Wald Distribution with Applications to Reliability Analysis

Abstract

 In this article, we develop neutrosophic extension of the Wald (Inverse Gaussian) 
distribution to present more realistic modelling for real data by introducing uncertainty in its 
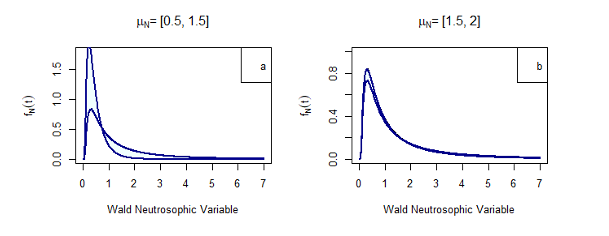
parameters. We derive fundamental statistical properties such as the probability density function 
(PDF), cumulative distribution function (CDF) and quantile function, and compare it with the 
classical model. This comparison shows the versatility and great robustness of the neutrosophic 
model against the imprecise data. Considering that the Wald distribution plays a significant role in 
the theory of reliability, we extend some key reliability functions into a neutrosophic framework. 
Under neutrosophic uncertainty, we derive and study the survival function, the reliability function 
and the hazard function which results in a more generalized and pragmatic approach for modeling 
reliability. These functions provide an improved decision-making process for situations in which 
classical models are unable to capture the inbuilt uncertainties of systems. To make it even more 
applicable, we propose an approach to generate random samples from neutrosophic Wald 
distribution using quantile function so that neutrosophic Wald distribution can be simulated and 
empirically validated. In addition, we also develop an estimation procedure through the method of 
moments (mom), which shows a simple way of estimating the parameters. 

DOI: 10.5281/zenodo.14969548