The extended study of 2-refined neutrosophic numbers
Keywords:
refined neutrosophic; square root; complex polynomial; real polynomial.Abstract
Numerical roots play a crucial role in real or complex equations, as well as in various
mathematical models involving differentiation, integration, and other mathematical relationships. In
the realm of mathematics, there is a growing trend of utilizing new formulas that incorporate non
classical numbers, such as neutrosophic and refined neutrosophic numbers. The objective of this
research is to establish precise and comprehensive mathematical procedures for dealing with refined
neutrosophic roots within mathematical formulas, be it equations or other mathematical constructs.
This paper presents an extensive study on 2-refined neutrosophic numbers, focusing on the square
root of a 2-refined neutrosophic real or complex number. Additionally, this work introduces the
concept of 2-refined neutrosophic real or complex polynomials and explores the process of finding
the refined neutrosophic roots to solve 2-refined neutrosophic equations. To illustrate these concepts,
several examples have been provided.
Downloads
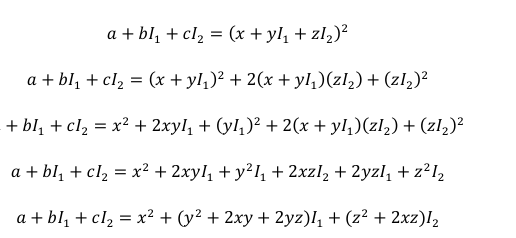
Downloads
Published
Issue
Section
License
Copyright (c) 2024 Neutrosophic Sets and Systems

This work is licensed under a Creative Commons Attribution 4.0 International License.







