“Deneutrosophication of Neutrosophic Bézier Surface Approximation Model

Abstract

The deneutrosophication process is a process transforming from neutrosophic values to
crisp output values. It is the final step for the operations within a neutrosophic set and system.
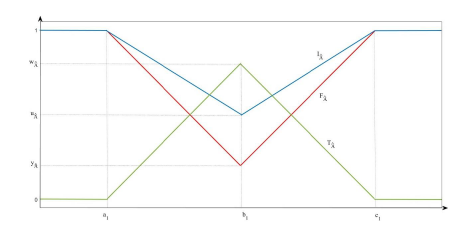
Neutrosophic set theories are a generalization of intuitionistic fuzzy and fuzzy set theories, focusing
on truth, indeterminacy, and falsity memberships independently. However, it isn't easy to generate
a geometrical model such as a Bézier surface by using neutrosophic set theory through the
deneutrosophication process. Therefore, this paper used an average of triangular footprint method
in the deneutrosophication process to construct the neutrosophic Bézier surface (NBS) models by
using approximation methods. Before generating the model, the neutrosophic control net (NCN)
must first be introduced using the deneutrosophication process. After that, the NCN will be blended
with the Bernstein basis function to generate the NBS approximation model. Next, some numerical
examples of NBS will be provided. Finally, the deneutrosophication of NBS approximation models
will be visualized, and its algorithm will be shown

DOI: 10.5281/zenodo.13564500