Neutrosophic Approach to Solving First-Order Differential Equations: Applications to Heat Convection with Uncertain Initial Conditions

Authors

  • Said Broumi Laboratory of Information Processing, Faculty of Science Ben M’Sik, University of Hassan II, Casablanca, Morocco
  • M. Shanmugapriya Department of Mathematics, Sri Sivasubramaniya Nadar College of Engineering, Chennai - 603 110, India
  • R. Sundareswaran Department of Mathematics, Sri Sivasubramaniya Nadar College of Engineering, Chennai - 603 110, India

Keywords:

difference equation; trapezoidal neutrosophic number, trapezoidal single valued neutrosophic number

Abstract

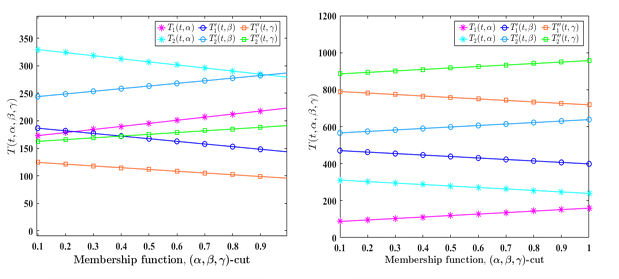
This study explores the solution of first-order differential equations  using trapezoidal neutrosophic numbers  as initial conditions. It examines various forms of  based on the dependencies of truth , indeterminacy , and falsity . The application first order DE is illustrated through heat conduction problems in fluids. The temperature distribution , , , ,  and  are analyzed through tables and graphs. A solution procedure for the system of first-order ODEs is developed and demonstrated with numerical examples.

 

DOI: 10.5281/zenodo.14538141

Downloads

Download data is not yet available.

Downloads

Published

2024-12-20

Issue

Vol. 79 (2025): Neutrosophic Sets and Systems

Section

Article

License

Copyright (c) 2024 Neutrosophic Sets and Systems

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

 Creative Commons Attribution (CC BY) license.

How to Cite

Said Broumi, M. Shanmugapriya, & R. Sundareswaran. (2024). Neutrosophic Approach to Solving First-Order Differential Equations: Applications to Heat Convection with Uncertain Initial Conditions. Neutrosophic Sets and Systems, 79, 419-435. https://fs.unm.edu/nss8/index.php/111/article/view/5594