Neutrosophic Approach to Solving First-Order Differential Equations:  Applications to Heat Convection with Uncertain Initial Conditions

Said Broumi; M. Shanmugapriya; R. Sundareswaran

Neutrosophic Approach to Solving First-Order Differential Equations: Applications to Heat Convection with Uncertain Initial Conditions

Authors

Said Broumi Laboratory of Information Processing, Faculty of Science Ben M’Sik, University of Hassan II, Casablanca, Morocco
M. Shanmugapriya Department of Mathematics, Sri Sivasubramaniya Nadar College of Engineering, Chennai - 603 110, India
R. Sundareswaran Department of Mathematics, Sri Sivasubramaniya Nadar College of Engineering, Chennai - 603 110, India

Keywords:

difference equation; trapezoidal neutrosophic number, trapezoidal single valued neutrosophic number

Abstract

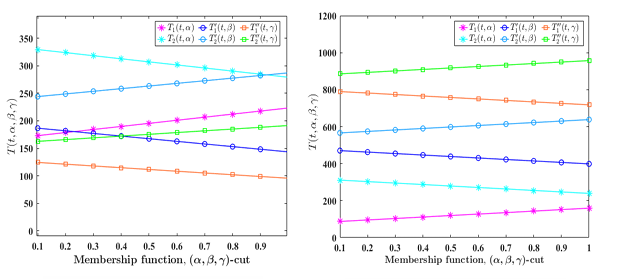
This study explores the solution of first-order differential equations using trapezoidal neutrosophic numbers as initial conditions. It examines various forms of based on the dependencies of truth , indeterminacy , and falsity . The application first order DE is illustrated through heat conduction problems in fluids. The temperature distribution , , , , and are analyzed through tables and graphs. A solution procedure for the system of first-order ODEs is developed and demonstrated with numerical examples.

DOI: 10.5281/zenodo.14538141

Downloads

Download data is not yet available.

Downloads

Published

2024-12-20

Issue

Vol. 79 (2025): Neutrosophic Sets and Systems

Section

Article

License

This work is licensed under a Creative Commons Attribution 4.0 International License.

Creative Commons Attribution (CC BY) license.

How to Cite

Said Broumi, M. Shanmugapriya, & R. Sundareswaran. (2024). Neutrosophic Approach to Solving First-Order Differential Equations: Applications to Heat Convection with Uncertain Initial Conditions. Neutrosophic Sets and Systems, 79, 419-435. https://fs.unm.edu/nss8/index.php/111/article/view/5594