Edge connectivity of a neutrosophic graph

Aparna Tripathy; Amaresh Chandra Panada; Siva Prasad Behera; Bhabani S. Mohanty

Authors

Aparna Tripathy Department of Mathematics, C.V. Raman Global University, Bhubaneswar-752054, Odisha, India.
Amaresh Chandra Panada Department of Mathematics, C.V. Raman Global University, Bhubaneswar-752054, Odisha, India
Siva Prasad Behera Department of Mathematics, C.V. Raman Global University, Bhubaneswar-752054, Odisha, India.
Bhabani S. Mohanty Department of Statistics and Applied Mathematics, Central University of Tamil Nadu, India

Keywords:

Cut-edge; Edge connectivity; Graph algorithms; Neutrosophic graph

Abstract

Neutosophic graphs are an extension of fuzzy and intuitionistic fuzzy graphs by
including the uncertainty, vagueness, and indeterminacy that are normal in the real
world. This paper looks into the edge connectivity of a neutrosophic graph, which is
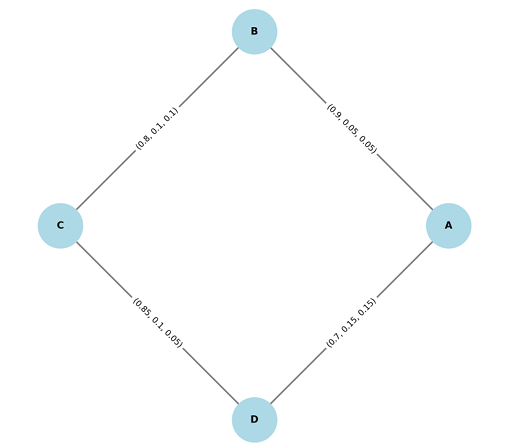
a basic parameter that shows how strong and fault-tolerant networks are that are
modelled by these graphs. Edge connectivity, which is the smallest number of edges
that need to be taken away from a graph to make it trivial or disconnected, is a key
concept in figuring out how strong and resilient networks are in many situations. This
paper also addresses computational challenges related to determining edge
connectivity in neutrosophic graphs. We develop efficient algorithms that minimize
computational overhead and ensure accuracy in identifying the critical edge sets. We
analyze the performance of these algorithms through both theoretical complexity
assessments and empirical evaluations on benchmark datasets. Some of the most
important things that the study found were critical edges that, when removed, have a
big effect on how connected the graph is and how indeterminacy affects the strength
of networks. The research underscores the importance of incorporating neutrosophic
parameters into graph connectivity studies to better model and analyse systems
characterized by uncertainty and partial knowledge.