Solving the shortest path Problem in an interval-valued Neutrosophic Pythagorean environment using an enhanced A* search algorithm

Abstract

The A* search algorithm is widely utilized to evaluate the shortest path in a given network. 
However, in a traditional A* search algorithm, the nodes are assumed to have crisp values, i.e., a 
single value. This assumption may not hold in many real-world scenarios where uncertainty or 
ambiguity is involved. In such cases, an interval-valued Neutrosophic Pythagorean (IVNP) 
environment can provide a more sound and accurate representation. Interval-valued Neutrosophic 
Pythagorean sets (IVNPS) are an effective way to model vague and imprecise data, which is prevalent 
in executive problems. These sets provide a more flexible way to capture uncertainty by allowing the 
values of nodes in the graph to vary within certain intervals rather than having fixed values. This 
interval representation can effectively handle imprecise or incomplete information and is a powerful 
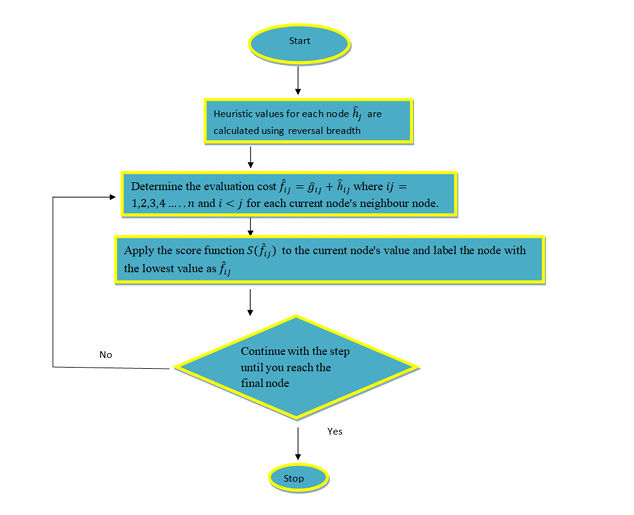
tool in executive processes. In this research paper, we proposed an improved A* search algorithm that 
takes advantage of the interval-valued neutrosophic Pythagorean environment. This algorithm aims 
to evaluate the shortest path in a graph under uncertainty and ambiguity. The proposed algorithm 
incorporates the IVNPS theory into the A* search framework to handle the uncertainty in node values 
and edge weights. It utilizes the concept of neutrosophic Pythagorean distance to calculate the 
heuristic function and make informed decisions on the next node to expand.

DOI: 10.5281/zenodo.14010229