Solving the Minimum Spanning Tree Problem Under Interval Valued Fermatean Neutrosophic Domain
Keywords:
Minimum Spanning Tree Problem; Fermatean Neutrosophic Domain; Dhouib-Matrix MSTP; Artificial Intelligence; Operations Research; Combinatorial OptimizationAbstract
In classical graph theory, the minimal spanning tree (MST) is a subgraph that lacks cycles
and efficiently connects every vertex by utilizing edges with the minimum weights. The
computation of a minimum spanning tree for a graph has been a pervasive problem over time.
However, in practical scenarios, uncertainty often arises in the form of fuzzy edge weights, leading
to the emergence of the Fuzzy Minimum Spanning Tree (FMST). This specialized approach is adept
at managing the inherent uncertainty present in edge weights within a fuzzy graph, a situation
commonly encountered in real-world applications. This study introduces the initial optimization
approach for the Minimum Spanning Tree Problem within the context of interval-valued fermatean
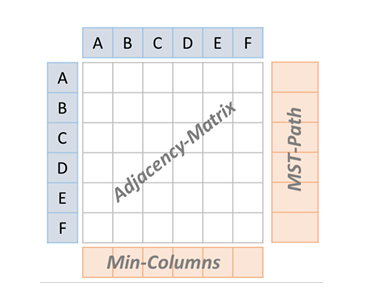
neutrosophic domain. The proposed solution involves the adaptation of the Dhouib-Matrix-MSTP
(DM-MSTP) method, an innovative technique designed for optimal resolution. The DM-MSTP
method operates by employing a column-row navigation strategy through the adjacency matrix. To
the best of our knowledge, instances of this specific problem have not been addressed previously.
To address this gap, a case study is generated, providing a comprehensive application of the novel
DM-MSTP method with detailed insights into its functionality and efficacy.
Downloads
Downloads
Published
Issue
Section
License
Copyright (c) 2024 Neutrosophic Sets and Systems

This work is licensed under a Creative Commons Attribution 4.0 International License.







