Implementation of Circle-Breaking Algorithm on Fermatean Neutrosophic Graph to discover Shortest Path

Abstract

In many scientific domains, there is a growing interest in the shortest path problem.
Traffic routes that can be precisely defined become arbitrary due to the damage that natural
catastrophes inflict on roads and bridges. The truth membership, indeterminacy membership,
and falsity membership of the component elements make up a neutrosophic set. Their axis of
symmetry is indeterminacy membership, and it has a symmetric form. The neutrosophic
number is a better way to express the edge distance in uncertain circumstances. With an edge
distance stated using Fermatean neutrosophic numbers (FrNN), the study aims to solve the
shortest path problem of the Fermatean neutrosophic graph. Additionally, the edge distance
will be resolved based on the score and precise functions derived from the FrNN. In order to
solve the shortest path problem and determine the shortest distance, the application of a
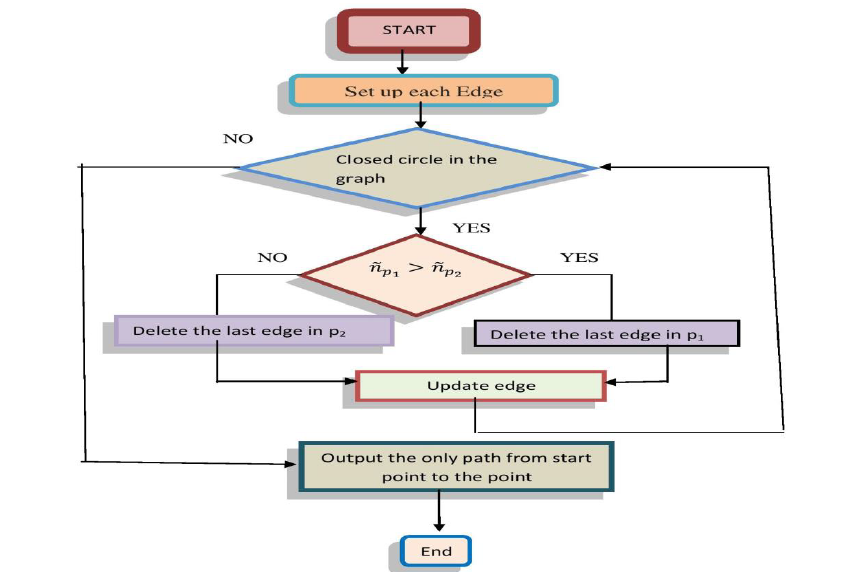
circle-breaking algorithm is suggested.

DOI: 10.5281/zenodo.13562206