On Solving Bi-objective Interval Valued Neutrosophic Assignment Problem

Abstract

The assignment problem (AP) is a well-researched combinatorial optimization problem in 
which the overall assignment cost or time is minimized by assigning multiple items (tasks) to several 
entities (workers). Today's optimization challenges cannot be adequately addressed by a 
single-objective AP, hence the bi-objective AP (BOAP) is taken into consideration. This problem 
frequently occurs in practical applications with ambiguous parameters in real life. Henceforth, in 
this article the uncertain parameters are presented as interval valued neutrosophic numbers. In the 
present study, we formulate bi-objectives assignment problem (BOAP) having cost and time 
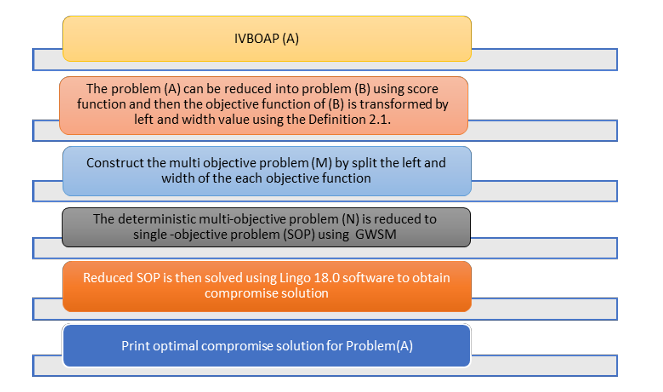
parameters as an interval valued neutrosophic numbers. We proposed interactive left-width method 
to solve the interval valued neutrosophic BOAP (IVNBOAP). In this method interval valued 
neutrosophic numbers is reduced to interval numbers using score function.  Then, the bi-objective 
interval assignment problem (BOIAP) is reduced to a deterministic BOAP using the left-width 
attributes on each objective function. The reduced deterministic objective function is separated and 
constructed as a multi-objective AP. In the solution procedure, the global weighted sum method is 
adopted to convert the multi-objective AP into a single objective problem (SOP) and solved using 
Lingo 18.0 software. Finally, numerical examples are illustrated to clarify the steps involved in the 
proposed method and results are compared with the other existing methods. 

DOI: 10.5281/zenodo.10729919