On Fixed Point Results in Neutrosophic Metric Spaces Using Auxiliary Functions
Keywords:
Fixed point; Neutrosophic set; Neutrosophic metric; (L )-contraction; Non linear contractionAbstract
In this paper, we establish novel xed point theorems in the framework of neutrosophic metric spaces
(NMS) by introducing the concept of neutrosophic (L )-contractions. These contractions generalize classical
contractive conditions by incorporating a function L that bounds the interaction between displacement terms
and a control function that modulates the contraction intensity. Under speci c hypothesis, we prove that
every neutrosophic (L )-contraction on a complete NMS admits a unique xed point. As applications, we
derive several corollaries by specifying the forms of L and , including cases where L is linear, additive, or
de ned via maximum functions. Our results unify and extend existing xed point theorems in neutrosophic
settings, while illustrative examples demonstrate their practical applicability
Downloads
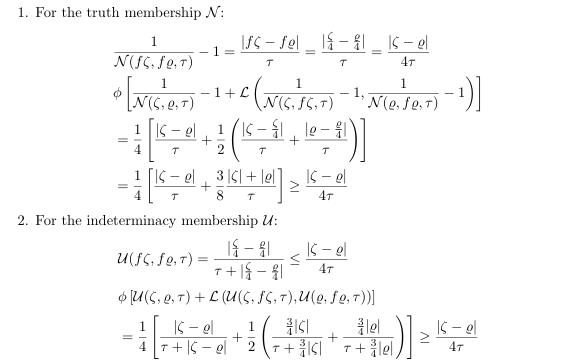
Downloads
Published
Issue
Section
License
Copyright (c) 2025 Neutrosophic Sets and Systems

This work is licensed under a Creative Commons Attribution 4.0 International License.






