Core Concepts Behind Quadripartitioned Neutrosophic Soft Block Matrices
Keywords:
Quadripartitioned Neutrosophic Soft Block Matrices; Soft Computing; Decision Science.Abstract
We introduce quadripartitioned neutrosophic soft block matrices, extending neutrosophic soft
matrices with a four-part structure to model uncertainty, indeterminacy, falsity, and a new
component: uncertainty, in decision-making. This enhancement overcomes limitations of
traditional neutrosophic soft matrices by comprehensively representing complex situations where
all four aspects must be simultaneously considered. Each matrix element is divided into four sub
components for a more nuanced analysis of the decision alternatives and criteria. The paper details
fundamental matrix operations (addition, subtraction, multiplication, and inversion) and explores
their properties. Case studies in decision support systems and optimization problems illustrate the
framework's applicability, particularly where traditional methods are insufficient. The model
proves especially valuable for complex decision-making in artificial intelligence, pattern
recognition, and fuzzy logic, handling multiple uncertainty layers. Finally, we examine the
theoretical basis and practical uses of quadripartitioned neutrosophic soft block matrices,
providing a new tool for soft computing and decision science.
Downloads
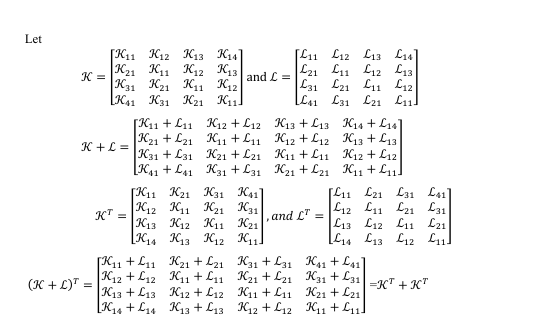
Downloads
Published
Issue
Section
License
Copyright (c) 2025 Neutrosophic Sets and Systems

This work is licensed under a Creative Commons Attribution 4.0 International License.






