Distance spectrum and energy in single valued neutrosophic  graphs

A.S. Sasipriya; Lakshmi Madireddy

Authors

A.S. Sasipriya Assistant professor, Faculty of Engineering and Technology, Datta Meghe Institute of Higher Education and Research, Wardha, Maharashtra, India.
Lakshmi Madireddy Assistant professor, Faculty of Engineering and Technology, Datta Meghe Institute of Higher Education and Research, Wardha, Maharashtra, India.

Keywords:

Single-valued neutrosophic graphs, distance matrix, distance energy, traveling salesman problem, neutrosophic sets, decision-making

Abstract

This study introduces the concept of distance matrix and distance energy in the context of
single valued neutrosophic graphs (SVNGs), which extend classical graph theory by incorporating
uncertainty and indeterminacy through neutrosophic sets. In SVNGs, edge weights are defined by
truth, indeterminacy, and falsity membership degrees, while the distance matrix captures the
shortest path lengths between vertex pairs. The distance energy, derived from the eigenvalues of this
matrix, reflects the structural properties of the graph under uncertainty. We establish theoretical
upper and lower bounds for the distance energy of SVNGs, offering insight into its behavior. To
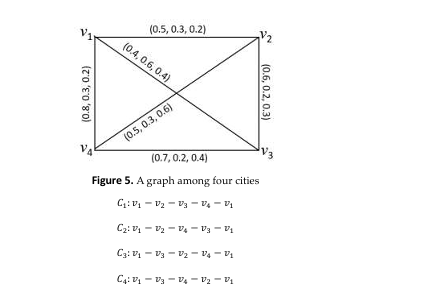
demonstrate practical utility, we apply this framework to the traveling salesman problem, modeling
it with an SVNG to account for uncertain travel costs. By computing and comparing the distance
energy of various paths, we rank them using a method that emphasizes truth while incorporating
indeterminacy and falsity. The results highlight the applicability of distance energy in uncertain
environments and underscore its value as a decision-support tool in optimization problems
involving imprecise or incomplete data.

DOI: 10.5281/zenodo.16340798