Characterization of interaction aggregating operators setting interval-valued Pythogorean neutrosophic set
Keywords:
weighted averaging, weighted geometric, generalized weighted averaging, generalized weighted geo metricAbstract
In this work, we present novel techniques for the interval-valued Pythogorean neutrosophic interac
tion aggregating operator. A hybrid of the neutrosophic set and the interval-valued Pythogorean fuzzy set. The
innovative averaging and geometric operations of interval-valued Pythogorean neutrosophic interaction numbers
are studied using aggregation operator. The interval-valued Pythogorean neutrosophic interaction is bounded
ness compatible, idempotent, associative, and commutative. Four new aggregating operators are introduced:
IPNI weighted averaging operator, interval-valued Pythogorean neutrosophic interaction weighted geometric
operator, generalized interval-valued Pythogorean neutrosophic interaction weighted averaging and generalized
interval-valued Pythogorean neutrosophic interaction weighted geometric.
Downloads
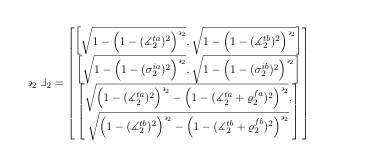
Downloads
Published
Issue
Section
License
Copyright (c) 2025 Neutrosophic Sets and Systems

This work is licensed under a Creative Commons Attribution 4.0 International License.


