Neutrosophic Quantum Theory: Partial Entanglement, Partial Effect of the Observer, and Teleportation

Abstract

 Quantum mechanics presents phenomena, such as entanglement and the observer effect, 
that challenge classical logical frameworks. Traditional binary and even fuzzy logic often prove 
insufficient in capturing the inherent imprecision, incompleteness, and indeterminacy prevalent in 
quantum systems. This article proposes a novel application of Neutrosophic Logic to describe 
partial entanglement and the partial effect of the observer in quantum physics experiments. By 
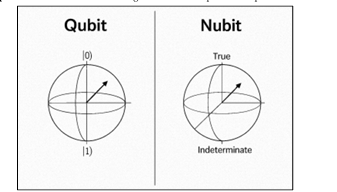
utilizing three independent components—Truth (T), Indeterminacy (I), and Falsity (F)—
 Neutrosophic Logic provides a comprehensive framework to represent quantum states that are 
neither fully correlated nor completely uncorrelated, but partially entangled. The degree of 
entanglement is modelled as T, separability as F, and intrinsic quantum uncertainty or decoherence 
as I. Furthermore, Neutrosophic Logic naturally accommodates observer-dependent truth values, 
aligning with the contextual nature of quantum measurements. This approach allows for a nuanced 
description where a quantum state can be simultaneously partially true, partially false, and partially 
indeterminate depending on the measurement basis or the act of observation. We argue that 
Neutrosophy offers a powerful philosophical and mathematical lens to better articulate the non
binary, fluid, and context-sensitive aspects of quantum reality, particularly where classical logic 
falters in capturing the essential "blurred areas" of quantum phenomena. 

DOI: 10.5281/zenodo.15426819