Construction Of Almost Unbiased Estimator For Population Mean Using Neutrosophic Information

Abstract

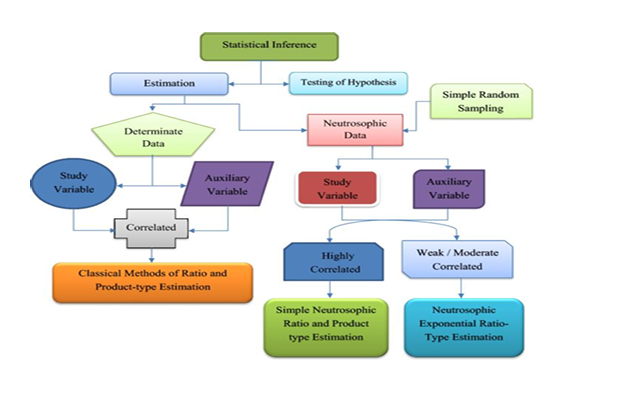
In classical statistics, the population mean is estimated using determinate, crisp data value when 
auxiliary information is known. These estimates can often be biased. The main objective of this study is to 
introduce the neutrosophic estimator with the minimum mean squared error (MSE) for the unknown value of 
the population mean as well as overcome the limitations of classical statistics when dealing with ambiguous 
or indeterminate data. Neutrosophic statistics was introduced by Florentin Smarandache. It is a generalisation 
of classical statistics that addresses ambiguous, unclear, vague, and indeterminate data. In this study, we have 
proposed neutrosophic almost unbiased estimator that use known neutrosophic auxiliary parameters to 
estimate the neutrosophic population mean of the primary variable. Equations for bias and mean squared error 
are calculated for the suggested estimators up to the first order of approximation. The proposed estimator 
performs better than the other existing estimators with respect to the MSE and percent relative efficiency 
(PRE) criteria. The estimator with the highest PRE or lowest MSE is advised for practical utility in various 
kinds of application areas. The theoretical conclusions are validated by the empirical analysis, which made 
use of the real data sets. 

DOI: 10.5281/zenodo.14010268