A Decision-Making Model for the Travelling Salesman Problem  Based on Neutrosophic Edge Connectivity

Aparna Tripathy; Amaresh Chandra Panda; Siva Prasad Behera; Prasanta Kumar  Raut; Said Broumi

Authors

Aparna Tripathy Department of Mathematics, C.V. Raman Global University, Bhubaneswar, Odisha, India.
Amaresh Chandra Panda Department of Mathematics, C.V. Raman Global University, Bhubaneswar, Odisha, India.
Siva Prasad Behera Department of Mathematics, C.V. Raman Global University, Bhubaneswar, Odisha, India.
Prasanta Kumar Raut Department of Mathematics, Trident Academy of Technology, Bhubaneswar, Odisha, India
Said Broumi Laboratory of Information Processing, Faculty of Science Ben M’Sik, University Hassan II, Casablanca, Morocco

Keywords:

Edge Connectivity; Neutrosophic Graph Theory; Optimization, Indeterminacy; Travelling Salesman Problem.

Abstract

Neutrosophic edge connectivity is a new idea in graph theory that adds indeterminacy and
uncertainty to traditional edge connectivity. It is especially useful for challenging
optimization problems that happen in the real world. The use of neutrosophic edge
connectivity in solving the well-known NP-hard issue in combinatorial optimization, the
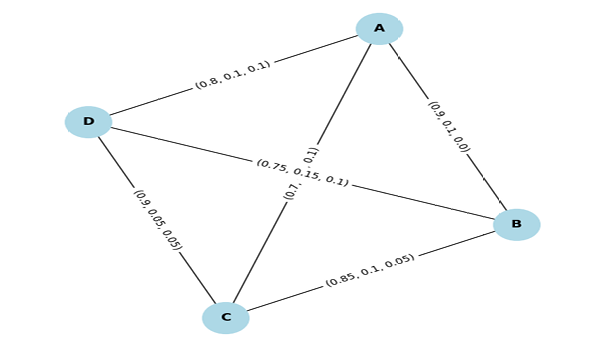
Travelling Salesman issue (TSP), is examined in this work. We make a new framework by
combining neutrosophic logic, which makes TSP solutions more flexible and realistic,
especially in environments that are uncertain and changing quickly, where traditional
deterministic models don't work. By taking into account the levels of truth, indeterminacy,
and falsity in edge connectivity, the suggested method helps people make better route optimization decisions. Here in this research paper, we provide a thorough theoretical study
along with mathematical examples of TSP (Traveling Salesman Problem) situations to verify
the method's efficiency. Furthermore, we proposed a problem statement. A logistics business
must choose the best delivery path among different cities. It turns out that our neutrosophic
based approach makes solutions more stable and opens up a beneficial path for more research
in real-world logistics and uncertainty-based optimization.

DOI: 10.5281/zenodo.16934803